こんにちは、くのへ@MasazaneKunoheです。
日曜日の機械紹介シリーズ。
今日は「PID制御」です。
PID制御ってご存じでしょうか?「フィードバック制御」のロジックです。
知識として知っている方は多いと思うんですが、いざ実装してみようとすると結構難しいんですよね~
今日はPID制御を紹介したいと思います。
こんなツイート頂きました
先日こんなツイート頂きました。
お風呂のお湯が安定的に出る仕組みはサーモスタットかな~
会社の温水生成用のバルブは、多分PID制御してるんじゃないかな~って思います。
2回に分けて紹介しようかな~と思ったんですが、サーモスタットの方は既存のイケてるWeb記事があり、どうしてもパクリに見えてしまいそうだったので、PID制御の方を説明したいと思います。
PID制御って何?
PID制御というのは「フィードバック制御」の一つです。
今回はご質問のお湯のシステムを考えてみましょう。
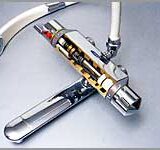
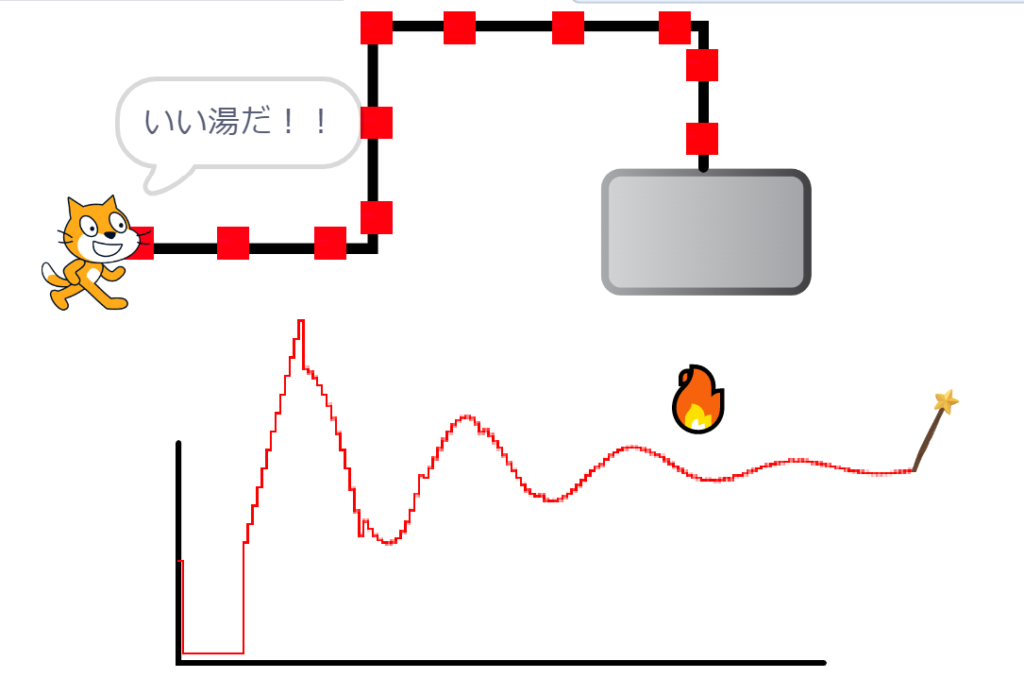
簡単なScratchプログラムを組んでみました。
右の鉄の箱っぽい物がボイラーです。ここからお湯が供給されますが、火が弱いときは冷たい水が来ます。
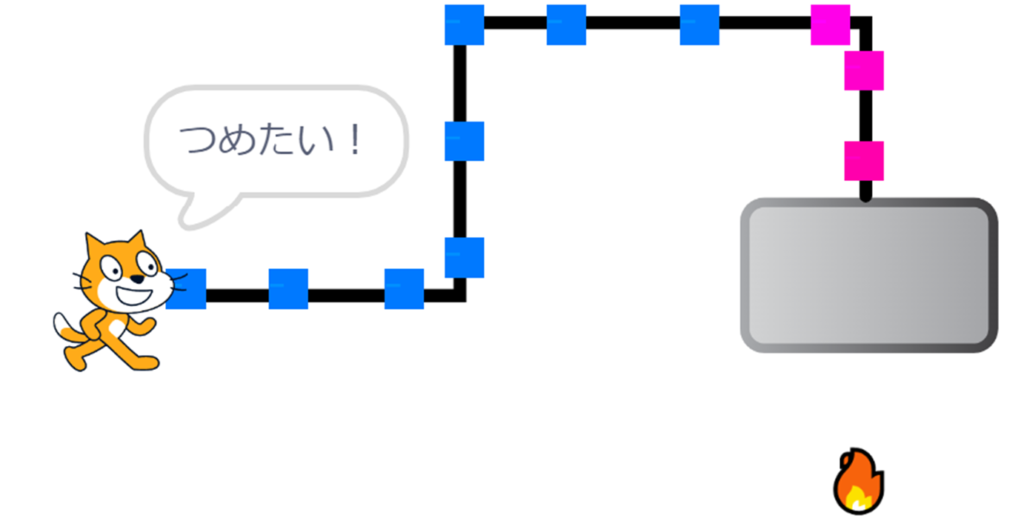
火が強いときは熱いお湯が来ます。
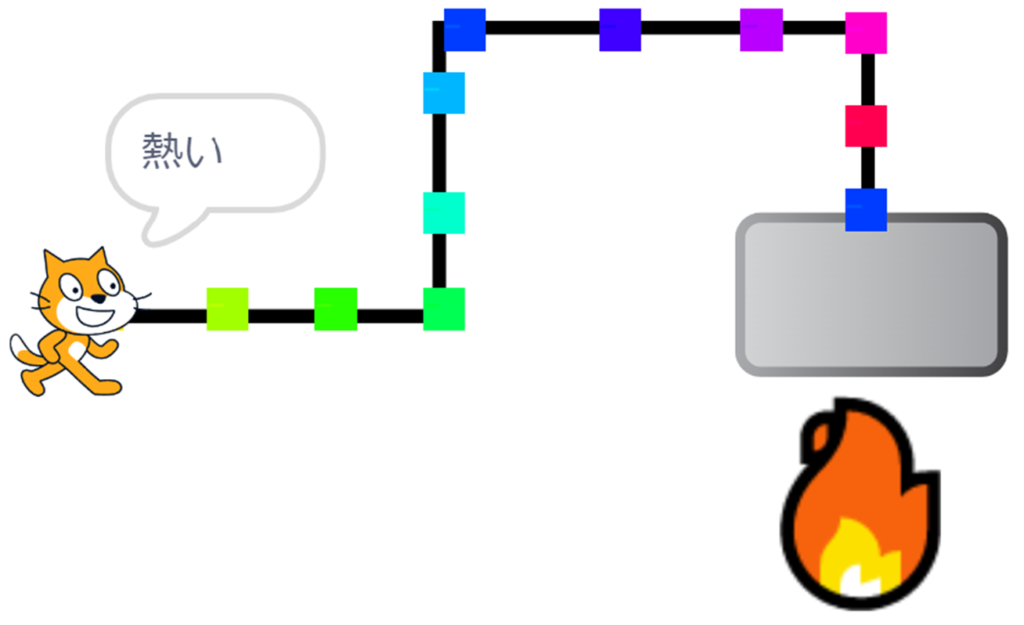
このように、冷たいときは火を強くしたいし、熱い時には火を弱めたくなります。
これがフィードバック制御の基本です。
プロセス値(:お湯の温度)をセット値(:40℃)に近づけたい場合、プロセス値とセット値の差をゼロにするように対象(:火)の大小をコントロールする方法です。
上手く制御できると、安定していいお湯が供給されます。
PID制御の説明は難しい、、、
PID制御はかなり昔から存在し、Web上にも多くの記事があります。
しかし、どれもちょっと難しいように思います。
WikipediaのPID制御の記事にあった式をお借りしてきました。(Wikipediaはこちら)
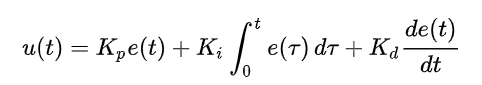
いや、これ分からんw
専門家の方はパッと見て分かると思いますが、これを制御関係者ではない人が見ても???だと思います。
PID制御というのは、P(比例)、I(積分)、D(微分)のことで、上記式の右辺の3つの項に該当します。
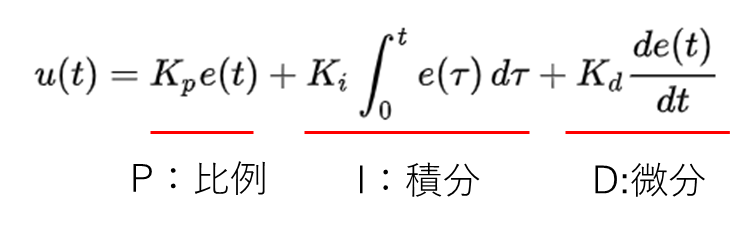
P:比例
目標値と現在の値の差を使う制御です。
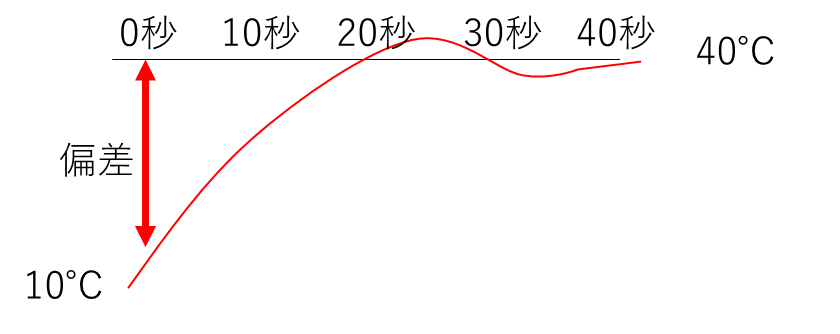
下の図の「偏差」と書いているところが、ボイラからお湯を出すときの0秒目のイメージです。
ボイラはまだ運転していないので、目標値と現在の値には大きな差がありますね。
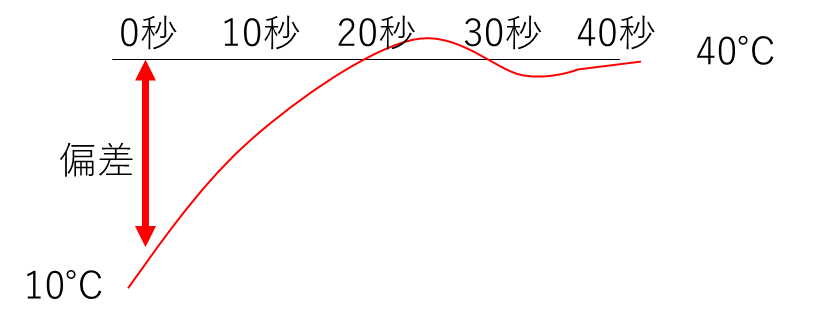
これを制御に使います。イメージは次の式です。
ボイラの炎量=目標値-現在の値
これで、目標と現在の値の差が大きいとガンガン追い焚きし、差が小さいと炎を弱める運転になります。
ただし、実際にはこれでは上手くいきません。
もう一度この式を見てください。
ボイラの炎量=目標値-現在の値
例えば目標値が40℃で、現在の値も40℃になったとしましょう。
すると、、、ボイラの炎の量が0になってしまいます。
すると当然ながらお湯の温度は下がり、、、またボイラの炎が灯ります。
この無限ループを防ぐためには、次の式のように「ゲイン」を設けます。
ボイラの炎量=ゲイン×(目標値-現在の値)
このゲインを0~1の間の数値にすることによって収束するようになります。
先ほど作った次の式がWikipediaに記載されていた右辺第1項になります。
ボイラの炎量=ゲイン×(目標値-現在の値)

しかし、ゲインを導入しても比例制御には問題があります。
目標値40℃に対し、収束値が到達していない状態で静定しています。
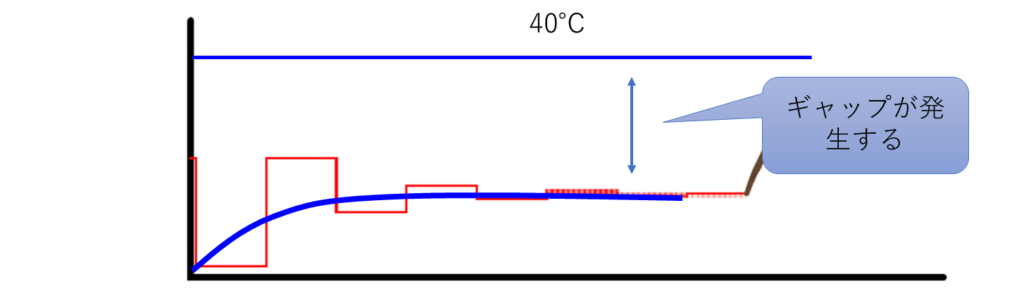
まあ、先ほどの式を見てみると分かります。
例えばゲインに0.5を入れると、、、ボイラの炎量は50%程度にしかなりません。
ボイラの炎量=ゲイン×(目標値-現在の値)
比例制御ではギャップが残ってしまう事がちょっとした課題になります。
I:積分
比例制御を補完するのが「積分」です。
次の図のように、偏差の面積を計算に使います。
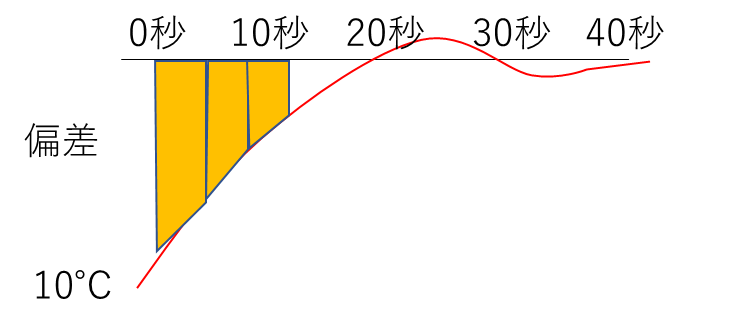
面積が下側に生成されれば追い焚きし、面積が上側に生成されれば炎を弱めることで、狙った温度にすることができます。
これがPI制御をした場合になります。いい感じに収束してくれています。
PI制御は非常によくできています。これで別に問題はなく使うことができます。
あえて問題点を挙げるとしたら、収束まで時間が掛かります。
そこで、スピーディに制御を静定させるために「微分」成分を入れることができます。
D:微分
制御の静定までの時間を短縮し、制御を素早く行わせるのが「微分」です。
下の図の模式図のように、温度が大きく変化する際はグラフが大きく傾き、変化が小さいときは傾きが小さくなります。
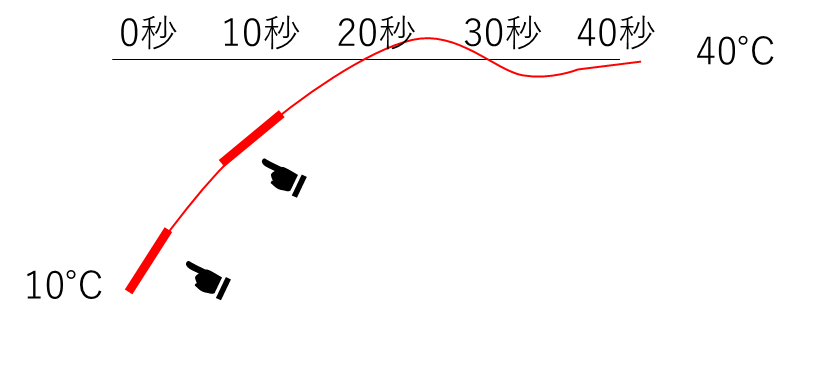
この特性を利用して、制御をブーストしてやるのです。ボイラの炎量調整に「傾き」の値を足してあげると、ふらつきが収まるのが早くなります。
微分の概念的な式はこちらになります。
ボイラの炎量=ゲイン×(偏差(現在)ー偏差(1秒前))÷1秒
ここで、上記式では「1秒」を基準に傾きを計算していますが、この刻みを無限に細かくすると微分になります。実際にはコンマ何秒のように小さい数字で刻みます。
ここまでがPID制御の基本理論になります。
実際には差分を足していきます
上記がPID制御の基本なのですが、Wikipediaの式には実装上の問題があります。
何が問題かというと、積分が問題なんです。
積分を計算するためには、ボイラを起動してから止めるまで、永遠とこの面積を積算し続ける必要があり、どのようなICチップでも記憶しきれません。
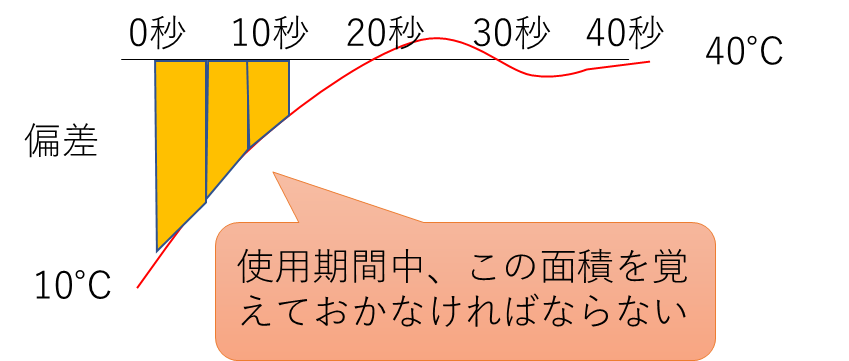
そこで、実際には差分を足していく方法が使われることが多いと思います。
具体的には、下の図を見てください。10秒時点の面積が青だとします。この青の面積をオレンジに足す計算をします。
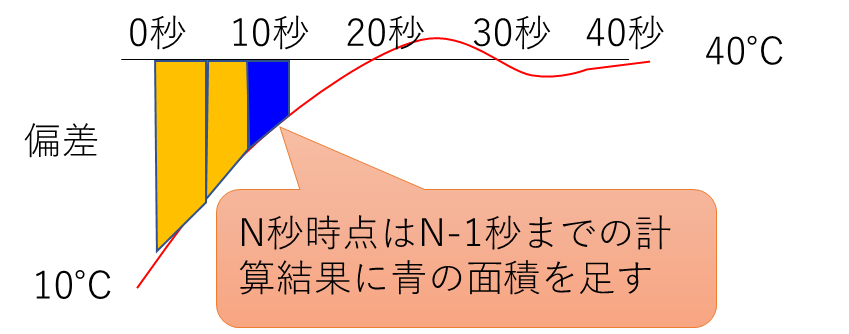
つまり、プログラム的に次の式を使うことでボイラ起動からN秒目までの面積Sが求められます。
M=M+S(N秒目)
(S(N秒目)は偏差×計算の時間間隔Δtで長方形に近似して求めることができる)
このように差分を使ってPID制御の式を書き換えると、次の式が得られます。

MV:制御目標値
Kp:ゲイン(比例成分)
Ki:ゲイン(積分成分)
Kd:ゲイン(微分成分)
これを使うとPID制御プログラムを組むことができます。
ScratchでPID制御プログラムを組んでみた
今回の説明ではScratchで作ったPID制御プログラムでシミュレートしてみました。
PID制御に関するコードはこちらになります。
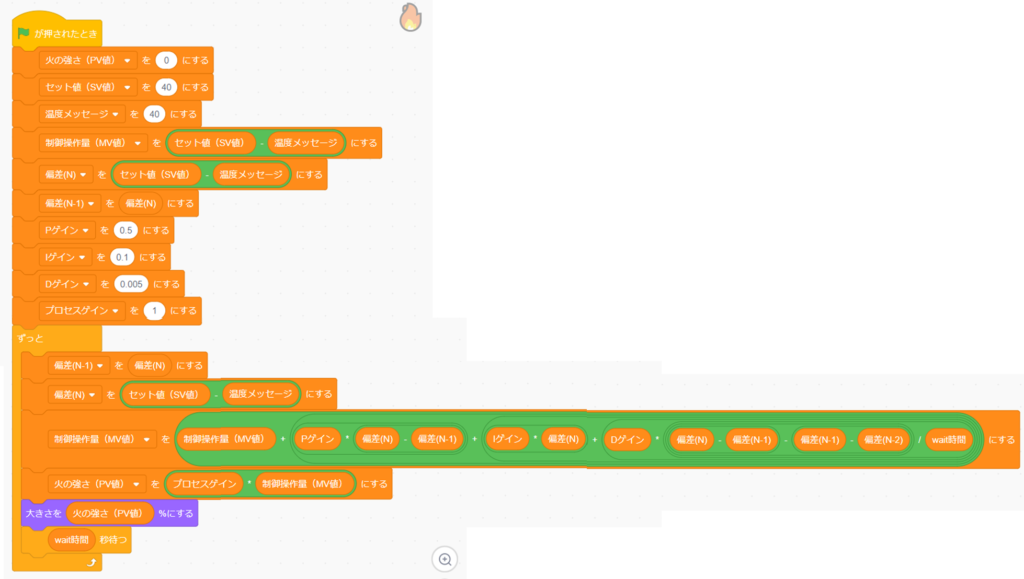
計器を制御部の近くに置こう
もう一つフィードバック制御の重要な点があります。 それは、計測点を制御部の近くに置くことです。
今回はネコを計器に見立てて、温度をフィードバックしてボイラの炎をコントロールしました。しかし、配管が長いので、実はネコに温水が届くまでに1.5秒くらいかかっています。
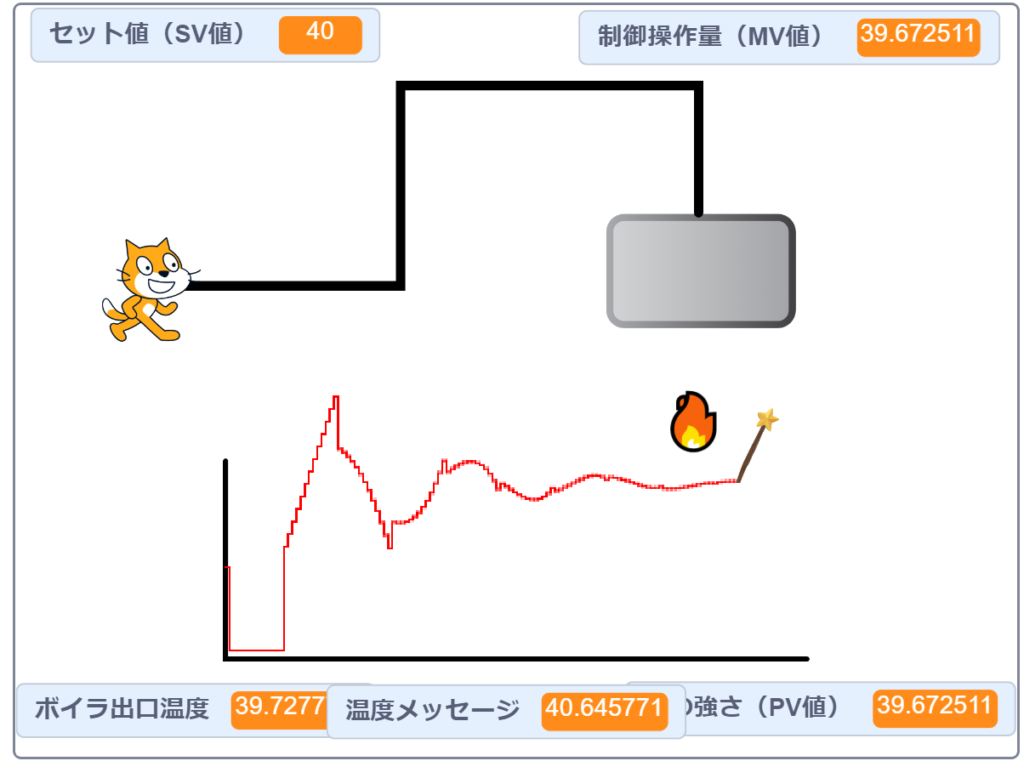
ここで、ネコ(計器)をボイラの近くに移動してみました。
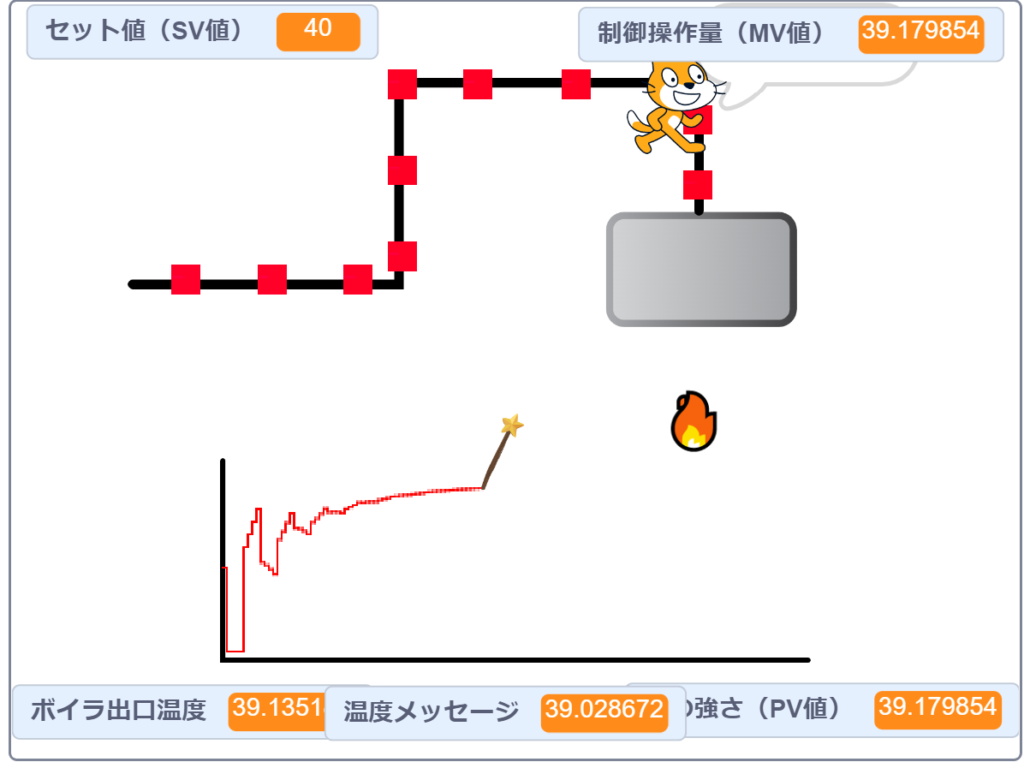
すると、温度のふらつきが収まるまでの時間がかなり短縮されましたね!
水の遅れ時間が制御の安定性にも影響するんですね~
以上。
今日はPID制御でした~
Scratchはこちらで公開していますので、興味ある方は見てみてください~
ではまた来週~
🦅バサバサ~
 くのへスタジオ
くのへスタジオ